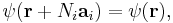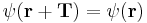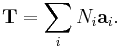Born–von Karman boundary condition
The Born–von Karman boundary condition is a set of boundary conditions which impose the restriction that a wave function must be periodic on a certain Bravais lattice. (Named after Max Born and Theodore Von Karman). This condition is often applied in solid state physics to model an ideal crystal.
The condition can be stated as
where i runs over the dimensions of the Bravais lattice, the ai are the primitive vectors of the lattice, and the Ni are any integers (assuming the lattice is infinite). This definition can be used to show that
for any lattice translation vector T such that:
Note, however, the Born–von Karman boundary conditions are useful when Ni are large (infinite).
The Born–von Karman boundary condition is important in solid state physics for analyzing many features of crystals, such as diffraction and the band gap. Modeling the potential of a crystal as a periodic function with the Born–von Karman boundary condition and plugging in Schrödinger's equation results in a proof of Bloch's theorem, which is particularly important in understanding the band structure of crystals.
References
- Neil W. Ashcroft, N. David Mermin (1976). Solid State Physics. Harcourt: Orlando..
- Leighton, Robert B. (1948). "The Vibrational Spectrum and Specific Heat of a Face-Centered Cubic Crystal". Reviews of Modern Physics 20 (1): 165–174. Bibcode 1948RvMP...20..165L. doi:10.1103/RevModPhys.20.165.